Laboratory Astrophysics by Caleb Ryder
Branching Ratio Measurements
 In Astrophysics, the study of the stellar evolution is of great significance. Furthering our understanding of how stars evolve increases our ability to understand the dynamics and principles which underlie all matter. Laboratory Astrophysics is the branch of physics which investigates specific aspects of stellar phenomena, specifically aimed at improving atomic data. The improved atomic data include branching fractions, atomic lifetimes and oscillator strengths, which are necessary to determine stellar abundance's (what the star is made of) and improve current nucleosynthesis models (which model the process of how a star fuses hydrogen into heavier elements).
In Astrophysics, the study of the stellar evolution is of great significance. Furthering our understanding of how stars evolve increases our ability to understand the dynamics and principles which underlie all matter. Laboratory Astrophysics is the branch of physics which investigates specific aspects of stellar phenomena, specifically aimed at improving atomic data. The improved atomic data include branching fractions, atomic lifetimes and oscillator strengths, which are necessary to determine stellar abundance's (what the star is made of) and improve current nucleosynthesis models (which model the process of how a star fuses hydrogen into heavier elements).
When an astrophysicist observes a star, he/she is able to detect certain characteristics which identify the star almost like a finger print; for example, the star's composition, the type of fusion occurring in its core, its size and temperature. Photons which originate within the star traverse outward through the photosphere (outermost surface of a star) and certain atoms interfere with the photons in this region and absorb the light, exciting the electrons in the atom. This photonic absorption causes the spectrum of emitted light to have "missing pieces" known as absorption bands. It is this spectrum, including emitted and non-emitted wavelengths of light, that is characteristic to a specific star and can be used to identify that star, the process is more commonly known as a spectral fingerprint.
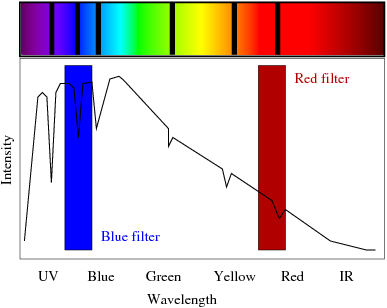
Simple Absorption Spectrum
Careful observation of this spectrum reveals that spectral lines have different intensities. It is these varying intensities that are of specific interest to my research. One could naively say that the larger the peak, the more abundant that element is (stellar abundance). However, further insight into the big picture of how these spectral lines are created leads us to understand that there are more complicated dynamics at work here than one would initially imagine. For example, a large peak could definitely arise because of a greater abundance of a particular element, but a large peak can also arise from a longer atomic lifetime (the duration of time an electron spends in an excited state before transitioning). This is exactly the predicament that astrophysicists deal with today.
Laboratory astrophysics aims to help with this dilemma, by studying electronic transitions to and from different energy levels (orbitals) within the atom, and producing more accurate atomic data. By shooting an optically focused laser onto a metalic surface, a plasma is created (~10,000 Kelvin) leaving behind an ablation site (crater) where a small portion of the metal has been highly energized and heated into a plasma. Neodymium (Nd) is the metal under investigation, due to its atomic properties which allow it to make many electronic transitions within energy levels under laser induced excitation. This created plasma is observed with a Spectrometer and the image from the ICCD is displayed a computer monitor looking like this.
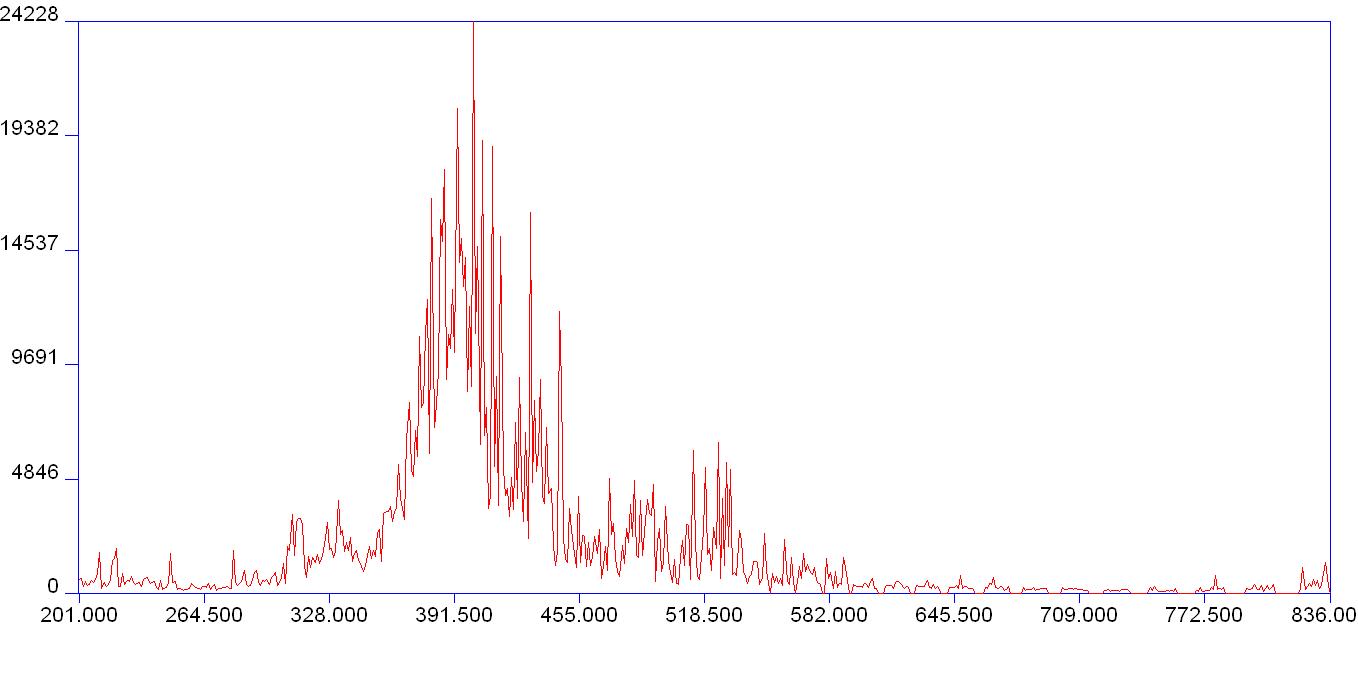 Nd emission spectrum
Nd emission spectrum
Branching ratios (or branching fractions) can be defined as the portion of electronic transitions that are made from a particular upper level down to a specific lower level divided by the total amount of electronic transitions from the same upper state to any lower level. An analogy of this would be to launch a large snowball onto a mountain top and observe how far down, from the initial ball, the resulting avalanches stream down the mountain (where snow represents electrons and the higher elevation represents more highly excited orbitals). The portion of electrons which descend into a specific lower energy level is a fraction of all the various branches descending from that particular upper level. Determining the branching ratios, Rij, directly enables us to know information about relative intensities, Iij, of a given energy level. (Aij is the Einstein spontaneous emission coefficient)
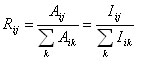
In order to determine the atomic lifetime of a given energy level, the intensities of given spectral emission lines are required. By determining the intensity of a particular electronic transition from a given upper level to a specific lower level and dividing this intensity by the sum of all the spectral intensities from that particular upper level, one determines the Branching ratio as displayed in the equation above.
Atomic Lifetime Measurements in Gallium (Ga)
In this part of my research I am measuring the lifetime duration for excited atoms in Gallium. Using Laser Induced Breakdown Spectroscopy (LIBS), as before, electrons in Gallium atoms are excited to various energy levels. These levels have a characteristic length of time for the atom to remain excited before its electrons de-excite back down to a lower energy state. I will focus specifically on measuring the atomic lifetime of the 4s5p3P2 level in Gallium. One of the transitions from this level emits photons at a wavelength of 541.6 nm; this photon is used as "starting-photon", detected using a photo multiplier tube, which will start a counter. When atoms exit this level and cascade down into another excited level it emits a second photon of different wavelength. This second photon ( wavelength = 633.407 nm) is detected using a photo multiplier tube and is used as the "stopping-photon" which stops the counter and gives the duration of the transition. Thus we detect the lifetime of the transition. This technique is better known as photon-coincidence technique.
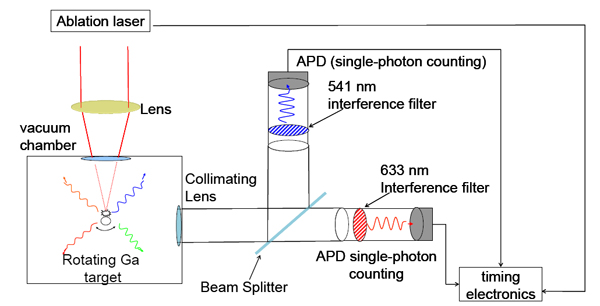
Schematic of Lifetime apparatus
